En el contexto del estudio sobre las Lentes Delgadas (Véase el artículo sobre la Ecuación de Gauss) definíamos el Aumento Lateral como "el cociente entre la altura de la imagen y la altura del sujeto".
No es necesario ser muy perspicaz para comprender que ambos conceptos son equivalentes.
Se definía este aumento lateral m de la siguiente manera:
y'
m = -----
y
donde y' era el tamaño de la imagen y donde y era el tamaño del sujeto.
En este mismo artículo se presentaba la denominada Ecuación de Gauss de una Lente Delgada:
1 1 1
---- + ---- = ----
s s' f
donde:
a) s es la distancia del sujeto al centro óptico de la lente.
b) s' es la distancia de la imagen al centro óptico de la lente.
c) f es la longitud focal de la lente.
En el artículo sobre Posición del plano imagen y aumento lateral se introducían dos importantes observaciones:
OBSERVACION 1:
Cuando el plano de enfoque se encuentra entre infinito (∞) y 2 veces la longitud focal, el plano imagen se encuentra a una distancia entre 1 y 2 longitudes focales.
OBSERVACION 2:
a) Si el plano de enfoque se encuentra entre ∞ y 2 veces la longitud focal se verifica que el aumento lateral m es menor que la unidad, lo cual significa que la imagen del sujeto es menor que el sujeto mismo. Esto es lo habitual en fotografía.
b) Si el plano de enfoque se encuentra a 2 veces la longitud focal se verifica que el aumento lateral m es igual a la unidad.
Atendiendo a este par de observaciones podría parecer que conseguir fotografías de aproximación (con ratios de reproducción entre 1:10 y 1:1) sería factible con cualquier objetivo. Para ello bastaría enfocar a una distancia algo superior a las 2 longitudes focales, lo cual nos garantizaría obtener aumentos laterales próximos a 1, o lo que es lo mismo que el tamaño de la imagen del sujeto fuera algo menor o incluso igual al tamaño del propio sujeto. Pero no es así.
El motivo es simplemente que los objetivos no pueden "enfocar" a distancias muy próximas. Dependiendo de casos, entre 5 y 15 veces la longitud focal. O lo que es lo mismo las propiedades convergentes de los objetivos no consiguen que los rayos de luz que salen de un punto próximo converjan en un único punto imagen.
Entonces: ¿Cómo lograr ratios de reproducción en el ámbito de la fotografía de aproximación?
Para entender cómo ésto puede hacerse, debemos partir de la Ecuación de Gauss.
1 1 1
Dado que --- + --- = --- si multiplicamos ambos miembros por s':
s s' f
s' s' s' s' s'
--- + --- = ---- o, lo que es igual: --- = --- - 1
s s' f s f
En la siguiente figura:
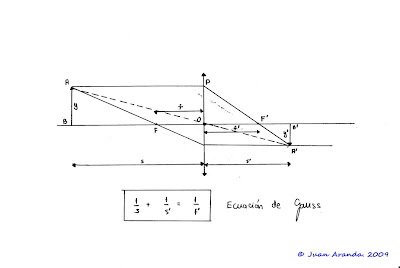
puede observarse que en los triángulos semejantes ABO y A'B'O se verifica que:
A'B' y' OB' s'
--- = --- = --- = ---
AB y OB s
y' s'
Por tanto m = --- = --- - 1
y f
Llegados a este punto, debe quedar claro que para aumentar m, sólo hay dos posibles caminos: O aumentamos s' o disiminuimos f.
Cada uno de los dispositivos que permiten obtener fotografías de aproximación opta por una de estas vías:
1) Anillos de extensión
Estos dispositivos se colocan entre el objetivo y el cuerpo de la cámara y su única misión es alejar el sensor del centro óptico del objetivo, aumentando por tanto el valor s'. Podréis encontrar muchos sitios en intenet donde se exponen fotografías de varios modelos.
2) Lentes de aproximación
Este dispositivo, de apariencia similar a un filtro y enroscable en la parte frontal del objetivo, tiene unas características ópticas más complejas y será explicado con detalle en un artículo posterior. Se basa en la disminución de la longitud focal.

