Lentes de Aproximación

Una lente de aproximación es una lente convergente que se ajusta como un filtro en el frontal del objetivo y que tiene como misión reducir la longitud focal del objetivo.
Las propiedades ópticas de una lente de aproximación se miden en dioptrías. Las dioptrías de una lente de aproximación se definen como la inversa de su longitud focal (medida en metros). Por tanto si disponemos, por ejemplo, de una lente de aproximación de 4 dioptrías, su longitud focal será de 1/4, es decir 0.25 m.
Lo cual significa obviamante que la longitud focal de esta lente será de 250 mm.
Para entender plenamente la influencia de una lente de aproximación deberemos simplificar un poco y asumir que tanto ésta como el propio objetivo son lentes delgadas. Aunque no es cierto, ésto nos proporcionará unos resultados aproximados.
En el artículo Fotografía de aproximación: Dispositivos dedujimos que la ratio de reproducción (o aumento lateral) venía dada por la ecuación:
             s'
  m  =  ----  -  1   (1)
             f
Así mismo, en el artículo Longitud Focal Efectiva dedujimos cuál era la longitud focal efectiva de dos lentes delgadas muy próximas entre sí. Si llamamos fo a la longitud focal del objetivo y fl a la longitud focal de la lente de aproximación, la fórmula que allí aparecería puede ser reescrita como:
               fo . fl
fefec =  --------- (2)
             fo +  fl
A partir de aquí vamos a trabajar con un caso concreto que nos va a permitir comprender la naturaleza de las lentes de aproximación. La figura que aparece al comienzo del artículo da cuenta de esta situación.
El objetivo Nikon 50 mm. f1.4 tiene una distancia mínima de enfoque de 450 mm. Imaginemos que enroscamos una lente de aproximación de 4 dioptrías, es decir de 250 mm.
Supongamos que ubicamos un sujeto a esa distancia particular, es decir 450 mm.
De la Ecuación de Gauss, escrita convenientemente:

           fo . s
s' =  ----------
           s  -  fo
tenemos que para el caso de  s = 450 mm. y fo = 50 mm.
          50. 450
 s' =  ----------  = 56.25
         450 - 50
Esto quiere decir que cuando la distancia de enfoque s es 450 mm, la imagen se forma en el sensor a 56.25 mm. del objetivo.
En estas circunstancias, la ratio de reproducción calculada por la fórmula (1) nos da:
         56.25
m  =  ------  - 1 = 0.125
           50
Este valor corresponde a una ratio de reproducción de 1:8, o lo que es lo mismo, la imagen es 8 veces menor que el propio sujeto.
Si ahora colocamos la lente de aproximación de 4 dioptrías, la situación cambia. ¿Por qué?. Porque ahora la longitud focal efectiva del conjunto disminuye. ¿No os lo creéis? Hagamos las cuentas.
                                                                 250 . 50
Por la fórumula (2) tenemos que   fefec = ------------ = 41.6 mm.
                                                                250 + 50
¿Qué influencia tiene ésto?
Si escribimos de otra manera la ecuación de Gauss:
         fefec
s = --------     . s'
       s' - fefec     
podemos calcular el valor al que podríamos ubicar un objeto que formase la imagen a la misma distancia s' (56.25 mm) en que se formaba cuando no habíamos colocado la lente de aproximación. Calculemos:
              41.6
s = -----------------   . 56.25  = 160 mm (aprox.)
       56.25  -  41.6
Esto significa que  podemos colocar un sujeto en esa posición que va a formar la misma imagen que formaba el sujeto original a 450 mm. Ahora bien, y ésto es lo importante, el objetivo "ve" un sujeto virtual colocado a 450 mm. Para él las cosas son como si no hubiera lente de aproximación y el sujeto estuviera colocado a 450 mm. Pero NO lo está. Esta situación se puede apreciar en el diagrama que encabeza el artículo.
¿Qué trascendencia tiene ésto en la ratio de reproducción? Pues calculemos:
                                                   56.25
El nuevo valor de m será  m =   ---------  - 1  = 0.350
                                                   41.6
Esto se correponde con una ratio de reproducción de (aprox.) 1:3. O lo que es lo mismo, el sujeto es 3 veces mayor que su imagen.
Todo ésto nos viene a decir que es la posibilidad de acercar el sujeto al objetivo lo que provoca un aumento en la ratio de reproducción. Eso sí, para el objetivo todo sucede como si el sujeto estuviese colocado mucho más lejos del objetivo y la ratio de reproducción fuese menor.

Longitud focal efectiva

Si tenemos dos lentes delgadas convergentes de longitudes focales respectivas f1 y f2, es fácil determinar cuáles es la longitud focal efectiva del conjunto, siempre y cuando la distancia d entre los centros ópticos de ambas lentes sea despreciable en relación con sus longitudes focales. Es decir, que ambas estén prácticamente en contacto. Esta será la situación cuando estudiemos el caso de las lentes de aproximación.
La ecuación de Gauss para la lente 1 será:
  1        1       1
---  +  --- = ---
  s1      s'1     f1
                                      1         1         1
De aquí se deduce que  ---  =  ---  -   ---     (1)
                                      s1        f1       s'1

La ecuación de Gauss para la lente 2 será:
  1         1          1
---  +  ----  =  ---
  s2      s'2         f2
                                      1         1       1
De aquí se deduce que  ---  =  ---  -  ---
                                      s'2       f2       s2
Pero como el punto imagen para la primera lente se convierte en el punto objeto para la segunda lente y la distancia se mide -para puntos objetos- desde el centro óptico hasta la izquierda, se verificará que s2 = -s'1.
                   1         1         1              1            1
Por tanto:  ---  =  ----  -  ---      =   ----  +   ----   (2)
                  s'2       f2      (-s'1)          f2          s'1

La ecuación de Gauss para la combinación de ambas lentes será:
   1             1          1
------  =  ----   +  ----
fefec          s1        s'2

Si sustituimos los valores de las ecuaciones (1) y (2) tendremos que:
    1            1        1
 -----  =   ---  + ----
  fefec        f1       f2
                                                       f1 f2
o lo que es lo mismo:      fefec =  -----------
                                                    f1 + f2

Esta ecuación nos permitirá deteminar la longitud focal efectiva de un objetivo al cual se le ha aclopado en su parte frontal una lente de aproximación.

Fotografía de aproximación: Dispositivos

En el ámbito de la Fotografía de Aproximación, el concepto más importante a tener en cuenta es el de Ratio de Reproducción, es decir, "la relación que existe entre el tamaño del sujeto real y el de su imagen en el sensor". (Véase el artículo sobre Fotografía de Aproximación).
En el contexto del estudio sobre las Lentes Delgadas (Véase el artículo sobre la Ecuación de Gauss) definíamos el Aumento Lateral como "el cociente entre la altura de la imagen y la altura del sujeto".
No es necesario ser muy perspicaz para comprender que ambos conceptos son equivalentes.
Se definía este aumento lateral m de la siguiente manera:
             y'
m   =  -----
             y
donde y' era el tamaño de la imagen y donde y era el tamaño del sujeto.
En este mismo artículo se presentaba la denominada Ecuación de Gauss de una Lente Delgada:
   1          1         1
 ----   + ----  =  ----
   s           s'         f
donde:
a) s es la distancia del sujeto al centro óptico de la lente.
b) s' es la distancia de la imagen al centro óptico de la lente.
c) f es la longitud focal de la lente.
En el artículo sobre Posición del plano imagen y aumento lateral se introducían dos importantes observaciones:
OBSERVACION 1:
Cuando el plano de enfoque se encuentra entre infinito (∞) y 2 veces la longitud focal, el plano imagen se encuentra a una distancia entre 1 y 2 longitudes focales.
OBSERVACION 2:
a) Si el plano de enfoque se encuentra entre ∞ y 2 veces la longitud focal se verifica que  el aumento lateral m es menor que la unidad, lo cual significa que la imagen del sujeto es menor que el sujeto mismo. Esto es lo habitual en fotografía.
b) Si el plano de enfoque se encuentra a 2 veces la longitud focal se verifica que el aumento lateral m es igual a la unidad.
Atendiendo a este par de observaciones podría parecer que conseguir fotografías de aproximación (con ratios de reproducción entre 1:10 y 1:1) sería factible con cualquier objetivo. Para ello bastaría enfocar a una distancia algo superior a las 2 longitudes focales, lo cual nos garantizaría obtener aumentos laterales próximos a 1, o lo que es lo mismo que el tamaño de la imagen del sujeto fuera algo menor o incluso igual al tamaño del propio sujeto. Pero no es así.
El motivo es simplemente que los objetivos no pueden "enfocar" a distancias muy próximas. Dependiendo de casos, entre 5 y 15 veces la longitud focal. O lo que es lo mismo las propiedades convergentes de los objetivos no consiguen que los rayos de luz que salen de un punto próximo converjan en un único punto imagen.
Entonces: ¿Cómo lograr ratios de reproducción en el ámbito de la fotografía de aproximación?
Para entender cómo ésto puede hacerse, debemos partir de la Ecuación de Gauss.
                    1         1       1
Dado que   ---  +  ---  = ---   si multiplicamos ambos miembros por s':
                    s         s'       f

 s'         s'      s'                                      s'      s'
---  +  --- = ----    o, lo que es igual:    --- = ---  - 1
  s         s'      f                                       s       f
En la siguiente figura:

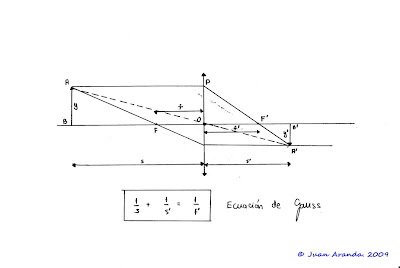
puede observarse que en los triángulos semejantes ABO y A'B'O se verifica que:

A'B'     y'     OB'     s'
--- =  ---  =  --- = ---
AB       y     OB      s
                       y'      s'
Por tanto m = ---  = ---  - 1
                       y       f     

Llegados a este punto, debe quedar claro que para aumentar m, sólo hay dos posibles caminos: O aumentamos s' o disiminuimos f.
Cada uno de los dispositivos que permiten obtener fotografías de aproximación opta por una de estas vías:
1) Anillos de extensión
    Estos dispositivos  se colocan entre el objetivo y el cuerpo de la cámara y su única misión es alejar el sensor del centro óptico del objetivo, aumentando por tanto el valor s'. Podréis encontrar muchos sitios en intenet donde se exponen fotografías de varios modelos.
2) Lentes de aproximación
    Este dispositivo, de apariencia similar a un filtro y enroscable en la parte frontal del objetivo, tiene unas características ópticas más complejas y será explicado con detalle en un artículo posterior. Se basa en la disminución de  la longitud focal.

Causas del desenfoque

Una fotografía puede estar desenfocada debido a una de tres causas:

a) Desenfoque debido a la profundidad de campo


Puerta de acceso. Edificio de la Universidad (Albacete)

En este tipo de casos el desenfoque es selectivo. Es decir, una parte de la fotografía aparece enfocada -aquella que se encuentra dentro de los límites de la profundidad de campo- y el resto aparece desenfocado. El fotógrafo selecciona el sujeto y lo aísla del entorno. En la imagen anterior se ha utilizado el objetivo Nikon 50mm. f1.4 que debido a su gran apertura máxima permite aislar una pequeña porción del resto de la escena. Los límites de la profundidad de campo se obtienen con un uso juicioso de tres parámetros diferentes:
Longitud focal, distancia de enfoque y apertura del diafragma. El uso del desenfoque selectivo es una herramienta de la mayor importancia en el proceso de concreción de la creatividad del fotógrafo.

b) Desenfoque debido al movimiento (trepidación) de la cámara.


Ciclistas. Ayna (Albacete)


Suele ser un error a la hora de capturar una fotografía. Lo más frecuente es que el deseo del fotógrafo sea estabilizar al máximo la cámara para evitar que ésto suceda. Pero hay ocasiones en que se puede utilizar como recurso creativo. De hecho, durante bastantes años, las exposiciones estaban llenas de fotografías intencionadamente movidas, debido a que de esta manera es posible conseguir un cierto aspecto de cuadro abstracto. Pero si se abusa de esta posibilidad, acaba por cansar. La inmensa mayoría de las fotografías que he obtenido en estas circunstancias las he considerado imágenes fallidas, pero en algún caso muy concreto, tal como la que encabeza este apartado, quizás podría apreciarse un cierto valor estético.

c) Desenfoque debido al movimiento del sujeto.


Plaza de Luis Camoens. Lisboa (Portugal)

Aquí las cosas están más claras. Si el sujeto principal de una fotografía está desenfocado debido a su propio movimiento, la toma ha devenido en fallo. No obstante, es importante comprender que otras partes de la escena pueden estar desenfocadas sin comprometer la validez de la fotografía. Un ejemplo bastante frecuente en que se puede observar esta situación es el que se corresponde con la fotografía que precede a este párrafo. Aquí el sujeto es la propia plaza y ha sido necesario utilizar un trípode y una velocidad de obturación larga, debido a la poca iluminación disponible. En estas circunstancias, las personas aparecerán desenfocadas si han realizado algún tipo de movimiento. Pero el sujeto principal no son ellas, sino la propia plaza. Y por tanto, su desenfoque no significa que la toma haya sido fallida.